斐波那契数列

来源Leetcode第509题斐波那契数列

斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N，计算 F(N)。

示例 1：

输入：2
输出：1

解释：F(2) = F(1) + F(0) = 1 + 0 = 1.

递归公式

就按公式来呗，用长度为3的数组保存

代码如下：

public int fib(int N) {
    if(N == 0) return 0;
    if(N == 1) return 1;
    
    int[] FIB = {1,1};
    while(N-- > 2) {
        FIB[1] = FIB[0] + FIB[1];
        FIB[0] = FIB[1] - FIB[0];
    }
    
    return FIB[1];
}

打表

提前存好结果，查表输出结果

代码如下：

public static final int[] FIB = {1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393,196418,317811,514229,832040,1346269,2178309,3524578,5702887,9227465,14930352,24157817,39088169,63245986,102334155,165580141,267914296,433494437,701408733,1134903170,1836311903};

public int fib(int N) {
    if(N == 0)
    return 0;
    return FIB[N-1];
}

矩阵运算

来源于上学期做的一个电路小实验

斐波那契(Fibonacci)数列中每项数值都是其两个直接前项的和，其生成规则如下公式1所示：

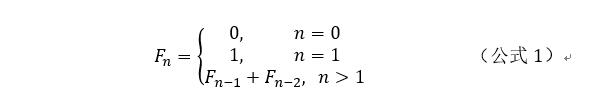
1.求Fibonacci数的矩阵算法
首先，对于数列的初始条件对应公式2的矩阵运算：

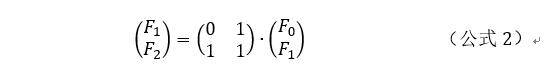
更一般化地，有公式3：

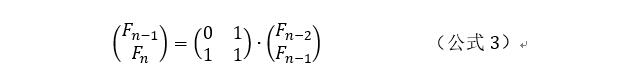
所以，根据递推关系可以得到公式4：

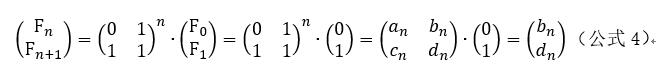
2.算法描述

Fibonacci(){
For (i=5 downto 0)
{
    if (Start==0) then 
{ 
if (n[i]==1) then Start=1; 
}
    Else
{ 
if (n[i]==1) 
then X=X2•A; 
else
 X=X2; }
}
return(X);
}

3.代码块

public int fib(int n) {

    if (n == 0) return 0;
    if (n == 1) return 1;

    int[][] X = new int[][]{new int[]{0, 1}, new int[]{1, 1}};
    int[][] A = new int[][]{new int[]{0, 1}, new int[]{1, 1}};
    int start = 0;
    String bin_n = Integer.toBinaryString(n);
    for (int i = 0; i < bin_n.length(); i++) {
        if(start == 0){
            if(bin_n.charAt(i) == '1')
                start = 1;
        }else
        {
            if(bin_n.charAt(i) == '1') {
                X = multiplyPower(X, 2);
                X = multiply(X,A);
            }
            else
                X = multiplyPower(X, 2);
        }
    }
    return X[0][1];
}


//矩阵快速幂
    public int[][] multiply(int [][]a,int[][]b){
        int[][]arr=new int[a.length][b[0].length];
        for(int i=0;i<a.length;i++){
            for(int j=0;j<b[0].length;j++){
                for(int k=0;k<a[0].length;k++){
                    arr[i][j]+=a[i][k]*b[k][j];
                }
            }
        }
        return arr;
    }

    public int[][] multiplyPower(int[][]a,int n){
        int[][] res=new int[a.length][a[0].length];
        for(int i=0;i<res.length;i++){
            for(int j=0;j<res[0].length;j++){
                if(i==j)
                    res[i][j]=1;
                else
                    res[i][j]=0;
            }

        }
        while(n!=0){
            if((n&1)==1)
                res=multiply(res,a);
            n>>=1;
            a=multiply(a,a);
        }
        return res;
    }