组合

来源Leetcode第77题组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

---

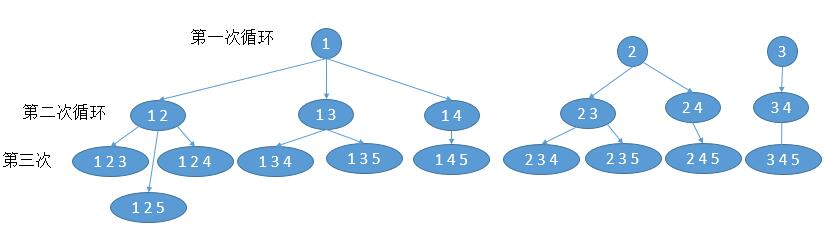
回溯

首先遍历从 first 到 n 的所有整数，将整数 i 添加到现有组合 curr 中，然后继续回溯向组合中添加更多整数，当组合完成，添加到输出中，并移去 i ，实现回溯。

代码如下：

int n;
int totals;
List<List<Integer>> output = new LinkedList();
public void backtrack( int first,LinkedList<Integer> curr){
    if(curr.size() == totals)
        output.add(new LinkedList(curr));

    for(int i = first;i < n + 1 ; ++i) {
        curr.add(i);
        backtrack(i + 1, curr);
        curr.removeLast();
    }
}

public List<List<Integer>> combine(int n, int k) {
    this.n = n;
    totals = k;
    backtrack(1,new LinkedList<Integer>());
    return output;
}

剪枝

优化for循环，没必要遍历到 n ，而是遍历到 n - k + output.size + 1,k - temp.size ( ) 代表我们还需要的数字个数。因为我们最后取到了 n，所以还要加 1。

代码如下:

int n;
int totals;
List<List<Integer>> ans = new ArrayList<>();
public void backtrack( int first,ArrayList<Integer> curr){
    if(curr.size() == totals){
        ans.add(new ArrayList<>(curr));
        return;
    }

    for(int i = first;i <= n - totals + curr.size() + 1 ; ++i) {
        curr.add(i);
        backtrack(i + 1, curr);
        curr.remove(curr.size() - 1);
    }
}

public List<List<Integer>> combine(int n, int k) {
    this.n = n;
    totals = k;
    backtrack(1,new ArrayList<Integer>());
    return ans;
}

迭代

来源于题解

完全按照解回溯的思想改成迭代。我们思考一下，回溯其实有三个过程。

• for 循环结束，也就是 i == n + 1，然后回到上一层的 for 循环
• temp.size() == k，也就是所需要的数字够了，然后把它加入到结果中。
• 每个 for 循环里边，进入递归，添加下一个数字

public List<List<Integer>> combine(int n, int k) {
    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
    for(int i = 0;i<k;i++){
        temp.add(0);
    }
    int i = 0;
    while (i >= 0) {
        temp.set(i, temp.get(i)+ 1); //当前数字加 1
        //当前数字大于 n，对应回溯法的 i == n + 1，然后回到上一层
        if (temp.get(i) > n) {
            i--;
        // 当前数字个数够了
        } else if (i == k - 1) { 
            ans.add(new ArrayList<>(temp));
        //进入更新下一个数字
        }else {
            i++;
            //把下一个数字置为上一个数字，类似于回溯法中的 start
            temp.set(i, temp.get(i-1));
        }
    }
    return ans;
}

迭代II

来源于题解

找 k 个数，我们可以先找出 1 个的所有结果，然后在 1 个的所有结果再添加 1 个数，变成 2 个，然后依次迭代，直到有 k 个数。

代码如下:

public List<List<Integer>> combine(int n, int k) {
    if (n == 0 || k == 0 || k > n) return Collections.emptyList();
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    //个数为 1 的所有可能
    for (int i = 1; i <= n + 1 - k; i++) res.add(Arrays.asList(i));
    //第一层循环，从 2 到 k
    for (int i = 2; i <= k; i++) {
        List<List<Integer>> tmp = new ArrayList<List<Integer>>();
        //第二层循环，遍历之前所有的结果
        for (List<Integer> list : res) {
            //第三次循环，对每个结果进行扩展
            //从最后一个元素加 1 开始，然后不是到 n ，而是和解法一的优化一样
            //(k - (i - 1） 代表当前已经有的个数，最后再加 1 是因为取了 n
            for (int m = list.get(list.size() - 1) + 1; m <= n - (k - (i - 1)) + 1; m++) {
                List<Integer> newList = new ArrayList<Integer>(list);
                newList.add(m);
                tmp.add(newList);
            }
        }
        res = tmp;
    }
    return res;
}

组合公式

C ( n, k ) = C ( n - 1, k - 1) + C ( n - 1, k )
从 n 个数字选 k 个，我们把所有结果分为两种，包含第 n 个数和不包含第 n 个数。这样的话，就可以把问题转换成：

• 从 n - 1 里边选 k - 1 个，然后每个结果加上 n
• 从 n - 1 个里边直接选 k 个。

代码如下:

public List<List<Integer>> combine(int n, int k) {
    if (k == n || k == 0) {
        List<Integer> row = new LinkedList<>();
        for (int i = 1; i <= k; ++i) {
            row.add(i);
        }
        return new LinkedList<>(Arrays.asList(row));
    }
    // n - 1 里边选 k - 1 个
    List<List<Integer>> result = combine(n - 1, k - 1);
    //每个结果加上 n
    result.forEach(e -> e.add(n));
    //把 n - 1 个选 k 个的结果也加入
    result.addAll(combine(n - 1, k));
    return result;
}